问题
问答题
设X1，X2，…，Xn(n＞2)为来自总体N(0，1)的简单随机样本，
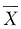为样本均值，记Yi=Xi-
=1，2，…，n．
求：(1)Yi的方差DYi，i=1，2，…．n；
(2)Y1与Y2的协方差Cov(Y1，Yn)．
答案
参考答案：根据简单随机样本的性质，X1，X2，…，Xn相互独立，且都服从分布
N(0，1)，EXi=0，DXi=1，i=1，2，…n．
[*]
(2) 因X1，X2，…，Xn相互独立，而独立的两个随机变量协方差等于零，于是有
[*]
而[*]又因[*]所以有
[*]
解析：[考点提示] 简单随机样本的性质的计算．