(1)当n=1时,有a13=a12,
由于an>0,所以a1=1.
当n=2时,有a13+a23=(a1+a2)2,
将a1=1代入上式,由于an>0,所以a2=2.
(2)由于a13+a23++an3=(a1+a2++an)2,①
则有a13+a23++an3+an+13=(a1+a2++an+an+1)2.②
②-①,得an+13=(a1+a2++an+an+1)2-(a1+a2++an)2,
由于an>0,所以an+12=2(a1+a2++an)+an+1.③
同样有an2=2(a1+a2++an-1)+an(n≥2),④
③-④,得an+12-an2=an+1+an.
所以an+1-an=1.
由于a2-a1=1,即当n≥1时都有an+1-an=1,所以数列{an}是首项为1,公差为1的等差数列.
故an=n.
(3)由(2)知an=n,则==(-).
所以Sn=+++++=(1-)+(-)+(-)++(-)+(-)=(1+--)=-(+).
∵Sn+1-Sn=>0,
∴数列{Sn}单调递增.
所以(Sn)min=S1=.
要使不等式Sn>loga(1-a)对任意正整数n恒成立,只要>loga(1-a).
∵1-a>0,∴0<a<1.
∴1-a>a,即0<a<.
所以,实数a的取值范围是(0,).

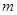 ,它们之间的动摩擦因数为μ。有界匀强磁场方向垂直纸面向里,磁感应强度大小为B。现对绝缘板施加一个水平向右、大小为μmg的恒力。当绝缘板即将离开磁场时,小物块恰好到达它的最左端,且对绝缘板无压力,此时绝缘板的速度是小物块速度的2倍。设滑动摩擦力等于最大静摩擦力。求:
,它们之间的动摩擦因数为μ。有界匀强磁场方向垂直纸面向里,磁感应强度大小为B。现对绝缘板施加一个水平向右、大小为μmg的恒力。当绝缘板即将离开磁场时,小物块恰好到达它的最左端,且对绝缘板无压力,此时绝缘板的速度是小物块速度的2倍。设滑动摩擦力等于最大静摩擦力。求: