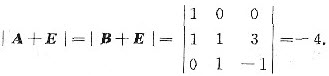问题
问答题
已知3阶矩阵A与三维向量x，使得向量组x，Ax，A2x线性无关，且满足A3x=3Ax-2A2x.
(1)记P=(x，Ax，A2x)，求3阶矩阵B，使A=PBP-1；(2)计算行列式|A+E|．
答案
参考答案：
方法1°由于AP=PB，即
A(x，Ax，A2x)=(Ax，A2x，A3x)=(Ax，A2x，3Ax-2A2x)
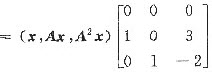
所以
方法2°由于P=(x，Ax，A2x)可逆，那么P-1P=E，即P-1(x，Ax，A2x)=E．
所以
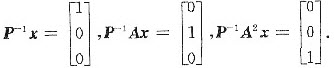
于是B=P-1AP=P-1(Ax，A2x，A3x)=P-1(Ax，A2x，3Ax-2A2x)
方法3°设
，则由AP=PB得
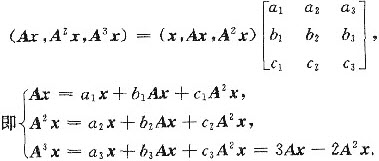
于是
因为x，Ax，A2x线性无关，故
a1=0，b1=1，c1=0；a2=0，b2=0，c2=1；a3=0，b3=3，c3=-2．
从而求出矩阵B．
(2)由(1)知A～B，那么A+E～B+E，从而
