问题
单项选择题
设(3-x)6=a0+a1x+a2x2+a3x3+a4x4+a5x5+a6x6,则a0+a2+a4+a6的值为()。
A.2040
B.2080
C.1096
D.4160
答案
参考答案:B
解析:
把已知等式两端的z分别换为1和-1,则得下列两式
(3-1)6=a0+a1+a2+a3+a4+a5+a6
①
(3+1)6=a0-a1+a2-a3+a4-a5+a6
②
①+②得26+46=2(a0+a2+a4+a6)
故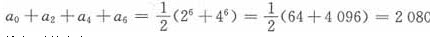
所以正确答案为B。
