参考答案：

由A=αβ^T和α^Tβ=0，有

A²=(αβ^T)(αβ^T)=α(β^Tα)β^T=0αβ^T=0．

(Ⅱ)设λ是A的任一特征值，η是A属于特征值λ的特征向量，即Aη=λη，η≠0．那么

A²=λAη=λ²η．

因为A²=O，故λ²η=0，又因η≠0，从而矩阵A的特征值是λ=0(n重根)．

不妨设向量α，β的第1个分量a₁≠0，b₁≠0．对齐次线性方程组(0E-A)x=0的系数矩阵作初等行变换，有

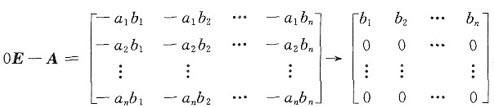
得到基础解系

η₁=(-b₂，b₁，…，0)^T，η₂=(-b₃，0，b₁，…，0)^T，…，η_n-1=(-b_n，0，0，…，b₁)^T．

于是矩阵A属于特征值λ=0的特征向量为

k₁η₁+k₂η₂+…+k_n-1η_n-1，其中k₁，k₂，…，k_n-1是不全为零的任意常数．