问题
问答题
已知二次型
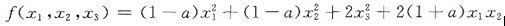的秩为2．
(Ⅰ)求a的值；
(Ⅱ)求正交变换x=Qy，把f(x1，x2，x3)化成标准形；
(Ⅲ)求方程f(x1，x2，x3)=0的解．
答案
参考答案：
(Ⅰ)二次型矩阵
，由于二次型f的秩为2，
即r(A)=2，所以有
(Ⅱ)当a=0时，由
知矩阵A的特征值是2，2，0．
对λ=2，由
得特征向量α1=(1，1，0)T，α2=(0，0，1)T．
对λ=0，由
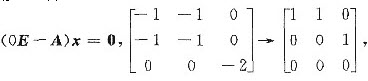
得特征向量α3(1，-1，0)T．
由于特征向量已经两两正交，只需单位化，于是有
令
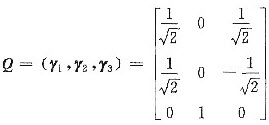，那么，经正交变换x=Qy有
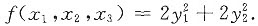
(Ⅲ)[方法一] 由(Ⅱ)知，在正交变换x=Qy下，f(x1，x2，x3)=0化成
，解之得y1=0，y2=0，y3=t(t为任意实数)，从而
即方程f(x1，x2，x3)=0的解是k(1，-1，0)T，k为任意实数．
[方法二] 由于
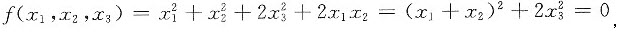，所以
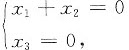
其通解为x=k(-1，1，0)T，其中k为任意常数．
