问题
问答题
设矩阵A与B相似,其中
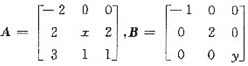
(1)求x和y的值,
(2)求可逆矩阵P,使P-1AP=B.
答案
参考答案:
(1)因为A和对角矩阵B相似,所以-1,2,y就是矩阵A的特征值

知λ=-2是A的特征值,因此必有y=-2.
再由λ=2是A的特征值,知|2E-A|=4[22-2(x+1)+(x-2)]=0,得x=0
(2)由
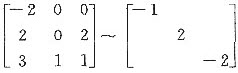
对λ=-1,由(-E-A)x=0得特征向量α1=(0,-2,1)T
对λ=2,由(2E-A)x=0得特征向量α2=(0,1,1)T
对λ=-2,由(-2E-A)x=0得特征向量α2=(1,0,-1)T
那么,令

