问题
问答题
设矩阵
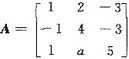的特征方程有一个二重根，求a的值，并讨论A是否可相似对角化．
答案
参考答案：
A的特征多项式为
若λ=2是特征方程的二重根，则有22-16+18+3a=0，解得a=-2．
当a=-2时，A的特征值为2，2，6，矩阵
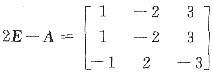的秩为1，故λ=2对应的线性无关的特征向量有两个，从而A可相似对角化．
若λ=2不是特征方程的二重根，则λ2-8λ+18+3a为完全平方，从而18+3a=16，
解得
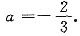
当
时，A的特征值为2，4，4，矩阵
的秩为2，故λ=4对应的线性无关的特征向量只有一个，从而A不可相似对角化．
