问题
问答题
设A为m阶实对称矩阵，B为m×n实矩阵，BT为B的转置矩阵，试证：BTAB为正定矩阵的充分必要条件是B的秩r(B) =n．
答案
参考答案：
[证明] 必要性．设BTAB为正定矩阵，按定义
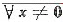，恒有xT(BTAB)x＞0．
因此，齐次线性方程组Bx=0只有零解，从而r(B)=n．
充分性．因(BTAB)T===BTAT(BT)T=BTAB，知BTAB为实对称矩阵．
若r(B)=n，则齐次方程组Bx=0只有零解，那么
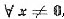必有Bx≠0．
又A为正定矩阵，所以对于Bx≠0，恒有(Bx)TA(Bx)＞0．
即当x≠0时，xT(BTAB)x＞0，故BTAB为正定矩阵．
