问题
问答题
设A为m×n实矩阵,E为n阶单位矩阵,已知矩阵B=λE+ATA,试证:当λ>0时,矩阵B为正定矩阵.
答案
参考答案:
[证明] 因BT=(λE+ATA)T=λE+ATA=B,故B是n阶实对称矩阵.构造二次型xTBx,则xTBx=xT(λE+ATA)x=λxTx+xTATAx=λxTx+(Ax)T(Ax).
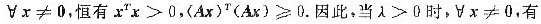
xTBx=2xTx+(Ax)TAx>0.
二次型为正定二次型,故B为正定矩阵.

设A为m×n实矩阵,E为n阶单位矩阵,已知矩阵B=λE+ATA,试证:当λ>0时,矩阵B为正定矩阵.
参考答案:
[证明] 因BT=(λE+ATA)T=λE+ATA=B,故B是n阶实对称矩阵.构造二次型xTBx,则xTBx=xT(λE+ATA)x=λxTx+xTATAx=λxTx+(Ax)T(Ax).
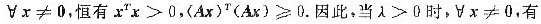
xTBx=2xTx+(Ax)TAx>0.
二次型为正定二次型,故B为正定矩阵.
