问题
问答题
设线性方程组
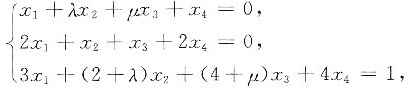
已知(1，-1，1，-1)T是该方程组的一个解．试求
(Ⅰ)方程组的全部解，并用对应的齐次方程组的基础解系表示全部解；
(Ⅱ)该方程组满足x2=x3的全部解．
答案
参考答案：
[解] 将(1，-1，1，-1)T代入方程组，得λ=μ．对增广矩阵作初等行变换，有
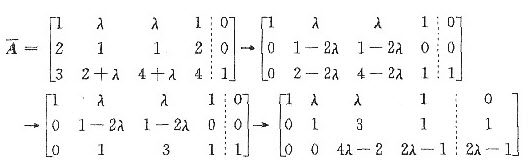
(Ⅰ)当
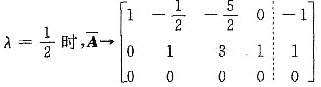
因
，方程组有无穷多解，其全部解为
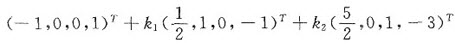，其中k1，k2为任意常数．
当 
因
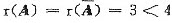，方程组有无穷多解，其全部解为
(-1，0，0，1)T+k(2，-1，1，-2)T，其中k为任意常数．
(Ⅱ)当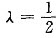 
时，若x2=x3，由方程组的通解
知1-3k1-2k2=k1，即
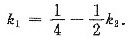
将其代入整理，得全部解为
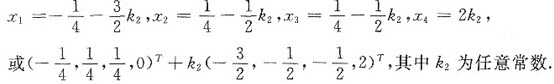
当
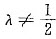时，x2=x3知-k=k，即k=0．从而只有惟一解(-1，0，0，1)T。