问题
问答题
设齐次线性方程组
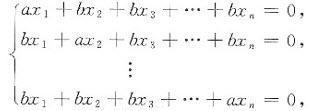
其中a≠0,b≠0,n≥2.试讨论a,b为何值时,方程组仅有零解,有无穷多组解在有无穷多组解时,求出全部解,并用基础解系表示全部解.
答案
参考答案:
[分析]: 这是n个未知数n个方程的齐次线性方程组,Ax=0只有零解的充分必要条件是|A|≠0,故可从计算系数行列式入手.
[解] 方程组的系数行列式
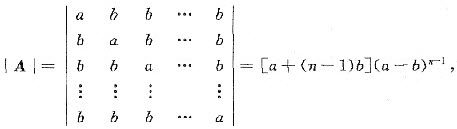
(1)当a≠b且a≠(1-n)b时,方程组只有零解.
(2)当a=b时,对系数矩阵作初等行变换,有
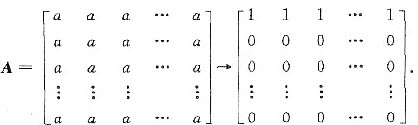
由于n-r(A)=n-1,取自由变量为x2,x3,…,xn得到基础解系为:
α1=(-1,1,0,…,0)T,α2=(-1,0,1,…,0)T,…,αn-1=(-1,0,0,…,1)T.
方程组的通解是:k1α1+k2α2+…+kn-1αn-1,其中k1,k2,…,kn-1为任意常数.
(3)当a=(1-n)b时,对系数矩阵作初等行变换,有

由于r(A)=n-1,有n-r(A)=1,即基础解系只有1个解向量,取自由变量为xn,则基础解系为α=(1,1,1,…,1)T.故通解为kα,(k为任意常数).
