参考答案：

[分析]： 如果β₁，β₂，…，β_s是Ax=0的基础解系，则表明

(1)β₁，β₂，…，β_s是Ax=0的解；

(2)β₁，β₂，…，β_s线性无关；

(3)s=n-r(A)或β₁，…，β_s可表示Ax=0的任一个解．

那么要证β₁，…，β_s是基础解系，也应当证这三点．本题中(1)、(3)是容易证明的，关键是(2)．线性相关性的证明在考研中是常见的．

[解] 由于β_i(i=1，2，…，s)是α₁，α₂，…，α_s的线性组合，又α₁，…，α_s是Ax=0的解，所以根据齐次方程组解的性质知β_i(i=1，2，…，s)均为Ax=0的解．

从α₁，α₂，…，α_s是Ax=0的基础解系，知s=n-r(A)．

下面来分析β₁，β₂，…，β_s线性无关的条件．设k₁β₁+k₂β₂+…+k_sβ_s=0，

即(t₁k₁+t₂k_s)α₁+(t₂k₁+t₁k₂)α₂+(t₂k₂+t₁k₃)α₃+…+(t₂k_s-1+t₁k_s)α_s=0，

由于α₁，α₂，…，α_s线性无关，因此有

因为系数行列式

所以当

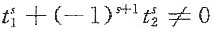时，方程组(*)只有零解k₁=k₂=…=k_s=0．从而β₁，β₂，…，β_s线性无关．即当s为偶数t₁≠±t₂，s为奇数，t₁≠-t₂时，β₁，β₂，…，β_s也为Ax=0的一个基础解系．