问题
单项选择题
设A为2阶矩阵，α1，α2为线性无关的2维列向量，Aα1=0，Aα2=2α1+α2，则A的非零特征值为（）．
A.1
B.2
C.3
D.4
答案
参考答案：A
解析：
根据已知条件本题有两种解法．用定义，由Aα1=0=0α1，A(2α1+α2)=2Aα1+Aα2=Aα2=2α1+α2，知A的特征值为1和0．因此A的非零特征值为1．或者利用相似，有
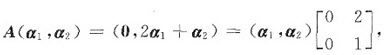
可知
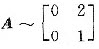，亦可得A的特征值1和0，因此A的非零特征值为1．
