参考答案：

(Ⅰ)设α₁，α₂，α₃是非齐次方程组的3个线性无关的解，那么α₁-α₂，α₁-α₃，是Ax=0线性无关的解，所以n-r(A)≥2，即r(A)≤2．

显然矩阵A中有2阶子式不为0，又有r(A)≥2，从而秩r(A)=2．

(Ⅱ)对增广矩阵作初等行变换，有

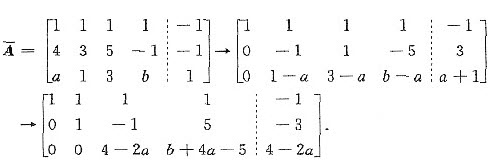
由题设和(Ⅰ)知，

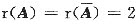，故有

4-2a=0，b+4a-5=0

解出a=2，b=-3

此时

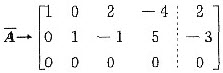
那么α=(2，-3，0，0)^T是Ax=b的解，且η₁=(-2，1，1，0)^T，η₂=(4，-5，0，1)是Ax=0的基础解系，所以方程组的通解是

α+k₁η₁+k₂η₂(k₁，k₂为任意常数)．

解析：

本题考查含参数的非齐次线性方程组的求解问题，那么如何求参数a和b题目给的追加信息是Ax=b有三个线性无关的解，如何用这信息其实问题(Ⅰ)r(A)=2就是提示。