问题
问答题
设有齐次线性方程组
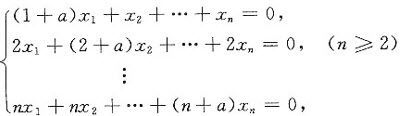
试问a为何值时,该方程组有非零解,并求其通解.
答案
参考答案:
[分析]: 确定参数,使包含n个未知量和n个方程的齐次线性方程组有非零解,通常用两个方法:一是对其系数矩阵作初等行变换化成阶梯形;再就是令其系数行列式为零求出参数值.本题的关键是参数a有两个值,对每个值都要讨论.
[解] 设齐次方程组的系数矩阵为A,则
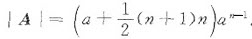
那么,Ax=0有非零解
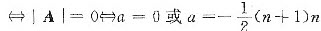
当a=0时,对系数矩阵A作初等变换,有
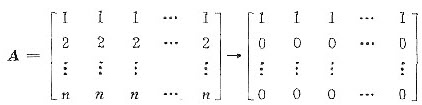
故方程组的同解方程组为x1+x2+…+xn=0,由此得基础解系为
η1=(-1,1,0,…,0)T,η2=(-1,0,1,…,0)T,…,ηn-1=(-1,0,0,…,1)T.
于是方程组的通解为x=k1η1+…+kn-1ηn-1,其中k1,…,kn-1为任意常数.
当
 时,对系数矩阵作初等行变换,把n行的-1倍分别加至每一行,有
时,对系数矩阵作初等行变换,把n行的-1倍分别加至每一行,有

故方程组的同解方程组为
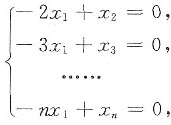 由此得基础解系为η=(1,2,…,n)T,于是方程组的通解为x=kη,其中k为任意常数.
由此得基础解系为η=(1,2,…,n)T,于是方程组的通解为x=kη,其中k为任意常数.

