问题
单项选择题
设向量β可由向量组α1,α2,…,αm线性表示,但不能由向量组(Ⅰ):α1,α2,…,αm-1线性表示,记向量组(Ⅱ):α1,α2,…,αm-1,β,则()
A.αm不能由(Ⅰ)线性表示,也不能由(Ⅱ)线性表示
B.αm不能由(Ⅰ)线性表示,可由(Ⅱ)线性表示
C.αm可由(Ⅰ)线性表示,也可由(Ⅱ)线性表示
D. αm可由(Ⅰ)线性表示,但不可由(Ⅱ)线性表示
答案
参考答案:B
解析:
因为β可由α1,α2,…,αm线性表示,故可设
β=k1α1+k2α2+…+kmαm.
由于β不能由α1,α2,…,αm-1线性表示,故上述表达式中必有km≠0.因此
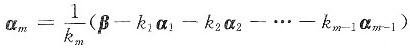
即αm可由(Ⅱ)线性表示,可排除(A)、(D).
若αm可由(Ⅰ)线性表示,设αm=l1α1+…+lm-1αm-1,则
β=(k1+kml2)α1+(k2+kml2)α2+…+(km-1+kmlm-1)αm-1.与题设矛盾,故应选(B).