问题
问答题
设αi=(ai1,ai2,…,ain)T(i=1,2,…,r;r<n)是n维实向量,且α1,α2,…,αr线性无关.已知β=(b1,b2,…,bn)T是线性方程组
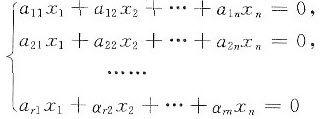
的非零解向量。试判断向量组α1,α2,…,αr,β的线性相关性.
答案
参考答案:
[解] 设k1α1+k2α2+…+krαr+lβ=0 (1)
因为β为方程组的非零解,有
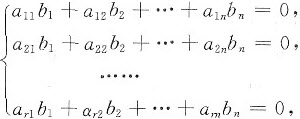
即β≠0,βTα1=0,…,βTαr=0。
用βT左乘(1),并把βTαi=0代入,得lβTβ=0.
因为β≠0,有βTβ>0,故必有l=0.
从而(1)式为k1α1+k2α2+…+krαr=0,由于α1,α2,…,αr线性无关,所以有
k1=k2=…=kr=0.
因此向量组α1,α2,…,αr,β线性无关.