问题
问答题
设有向量组(Ⅰ)：α1=(1，0，2)T，α2=(1，1，3)T，α3=(1，-1，a+2)T和向量组(Ⅱ)：β1=(1，2，a+3)T，β2=(2，1，a+6)T，β3=(2，1，a+4)T．试问：当a为何值时，向量组(Ⅰ)与(Ⅱ)等价当a为何值时，向量组(Ⅰ)与(Ⅱ)不等价
答案
参考答案：
[分析]： 所谓向量组(Ⅰ)与(Ⅱ)等价，即向量组(Ⅰ)与(Ⅱ)可以互相线性表出．若方程组x1α1+x2α2+x3α3=β有解，即β可以由α1，α2，α3线性表出．若对同一个a，三个方程组x1α1+x2α2+x3α3=βi(i=1，2，3)均有解，即向量组(Ⅱ)可以由(Ⅰ)线性表出．
[解] 设x1α1+x2α2+x3α3=βi(i=1，2，3)，由于这三个方程组的系数矩阵一样，故可拼成一个大的增广矩阵统一的加减消元．对(α1，α2，α3┆β1，β2，β3)作初等行变换，有
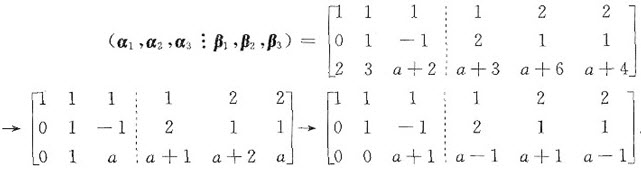
(1)当a≠-1时，行列式|α1，α2，α3|=a+1≠0，由克拉默法则，知三个线性方程组x1α1+x2α2+x3α3=βi(i=1，2，3)均有唯一解．所以，β1，β2，β3可由向量组(Ⅰ)线性表出。
由于行列式
故
a，方程组x1β1+x2β2+x3β3=αj(i=1，2，3)恒有唯一解，即α1，α2，α3总可由向量组(Ⅱ)线性表出．
因此，当a≠-1时，向量组(Ⅰ)与(Ⅱ)等价．
(2)当a=-1时，有
由于秩r(α1，α2，α3)≠r(α1，α2，α3，β1)，线性方程组x1α1+x2α2+x3α3=βi无解，故向量β1不能由α1，α2，α3线性表出．因此，向量组(Ⅰ)与(Ⅱ)不等价．