（1）由f(x)=x2-ax，当x∈(-1，1)时，f(x)＜

1

2

得：变形为：x2-

1

2

＜ax，构造函数：g(x)=x2-

1

2

，h(x) = ax，其中x∈(-1，1)，a＞0，且a≠1

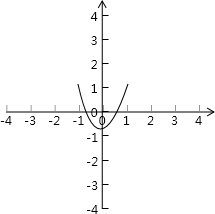
（2）由函数图象知，当x∈（-1，1）时，

g（x）的图象在h（x）的图象下方．

如图：①当a＞1时，有h（-1）≥g（-1），

即a-1≥(-1)2-

1

2

，得a≤2，即1＜a≤2；

②当1＞a＞0时，有h(1)≥g(1)，即a≥12-

1

2

，得a≥

1

2

.即

1

2

≤ a＜1.

有①、②知：实数a的取值范围是[

1

2

，1）∪（1，2]．

答案为[

1

2

，1）∪（1，2]．