问题
解答题
已知:直线y=kx(k≠0)经过点(3,-4).
(1)求k的值;
(2)将该直线向上平移m(m>0)个单位,若平移后得到的直线与半径为6的⊙O相离(点O为坐标原点),试求m的取值范围.
答案
(1)依题意得:-4=3k,
∴k=-
.(3分)4 3
(2)由(1)及题意知,设平移后得到的直线l所对应的函数关系式为y=-
x+m(m>0).(4分)4 3
设直线l与x轴、y轴分别交于点A、B,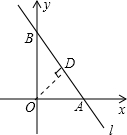 如右图所示
如右图所示
当x=0时,y=m;当y=0时,x=
m.3 4
∴A(
m,0),B(0,m),即OA=3 4
m,OB=m.3 4
在Rt△OAB中,AB=
2=OA2+OB2
=
m2+m29 16
m.(5分)5 4
过点O作OD⊥AB于D,
∵S△ABO=
OD•AB=1 2
OA•OB,1 2
∴
ODו1 2
m=5 4
ו1 2
m•m,3 4
∵m>0,解得OD=
m(6分)3 5
∵直线与半径为6的⊙O相离,
∴
m>6,解得m>10.3 5
即m的取值范围为m>10.(8分)
