设y=y(x)是二阶常系数线性微分方程y"+2my’+n2y=0满足y(0)=a与y’(0)=b的特解,其中常数m>n>0,a≠b,则
 =______.
=______.
参考答案:
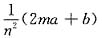
解析: 二阶方程y"+2my’+n2y=0的特征方程是λ2+2mλ+n2=0,特征根是λ1=-m+
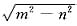 =-(m-
=-(m-
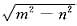 )<0,λ2=-m-
)<0,λ2=-m-
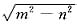 <0,由此可见,微分方程y"+2my’+n2y=0的任何一个解y=C1eλ1x+C2eλ2x都满足
<0,由此可见,微分方程y"+2my’+n2y=0的任何一个解y=C1eλ1x+C2eλ2x都满足
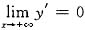 .
.
若y=y(x)是方程满足初值y(0)=a,y’(0)=b的特解,则

故
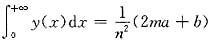 .
.
设y=y(x)是二阶常系数线性微分方程y"+2my’+n2y=0满足y(0)=a与y’(0)=b的特解,其中常数m>n>0,a≠b,则
 =______.
=______.
参考答案:
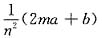
解析: 二阶方程y"+2my’+n2y=0的特征方程是λ2+2mλ+n2=0,特征根是λ1=-m+
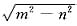 =-(m-
=-(m-
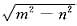 )<0,λ2=-m-
)<0,λ2=-m-
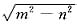 <0,由此可见,微分方程y"+2my’+n2y=0的任何一个解y=C1eλ1x+C2eλ2x都满足
<0,由此可见,微分方程y"+2my’+n2y=0的任何一个解y=C1eλ1x+C2eλ2x都满足
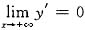 .
.
若y=y(x)是方程满足初值y(0)=a,y’(0)=b的特解,则

故
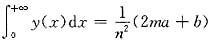 .
.