问题
填空题
设D=(x，y)|-1≤x≤1，0≤y≤2，则二重积分I=
=______．
答案
参考答案：
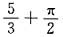
解析： 这是带有绝对值的二重积分，可通过分割积分区域的办法去掉绝对值符号．
如图，将区域D分成D1和D2两部分，其中
D1={(x，y)|-1≤x≤1，0≤y≤x2}，
D2={(x，y)|-1≤x≤1，x2≤y≤2}，
(x，y)∈D1时，
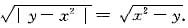
(x，y)∈D2时，
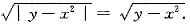所以
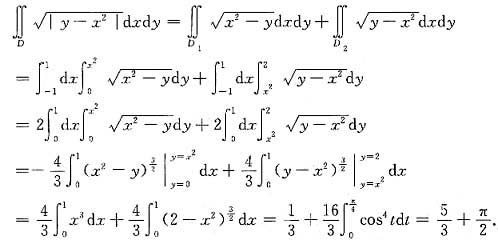
在计算中利用了积分区域D1与D2关于y轴的对称性以及被积函数
与
都是x的偶函数