问题
填空题
差分方程yt+1 +5yt-3t2+t=0的通解为______.
答案
参考答案:C(-5)t+
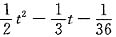
解析: 按照差分方程设解的规则,可设方程的通解为
yt=C(-5)t+αt2+βt+γ,
其中C为任意常数,α,β与γ为待定常数,于是
yt+1=-5C(-5)t+α(t+1)2+β(t+1)+γ,
代入差分方程可得
yt+1+5yt=6(at2+βt+γ)+α(2t+1)+β
 3t2-t,
3t2-t,
于是有6α=3,6β+2α=-1,6γ+α+β=0
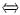 α=
α=
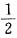 ,β=
,β=
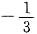 ,γ=
,γ=
 .故差分方程的
.故差分方程的
通解为yt=C(-5)t+
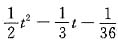 ,
,
其中C是任意常数.
