问题
填空题
设函数f(t)在[0,+∞)上连续,且满足方程f(t)=t2+
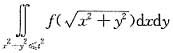 则f(t)=______.
则f(t)=______.
答案
参考答案:
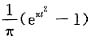
解析: 由于等式两边都含有未知函数f(t),要求出f(t)的表达式,必须对等式两边求导数得到一个微分方程,再解此微分方程即可得到f(t)的表达式.
注意等式右侧含有二重积分,积分区域D是以原点为中心,半径为t的圆域x2+y2≤t2,被积函数
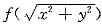 是以x2+y2为变量的函数,可化为极坐标系下的二重积分来计算.
是以x2+y2为变量的函数,可化为极坐标系下的二重积分来计算.
令x=rcosθ,y=rsinθ,则
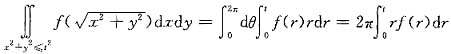
于是f(t)=t2+2π
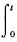 rf(r)dr,两边对t求导得一阶线性微分方程f’(t)=2t+2πtf(t),可
rf(r)dr,两边对t求导得一阶线性微分方程f’(t)=2t+2πtf(t),可
解得
f(t)=Ceπt2-
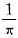 .
.
又由原方程得f(0)=0,由此可确定常数C=
 .
.
于是f(t)=
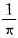 (eπt2-1).
(eπt2-1).
