问题
填空题
已知y1=cos2x-
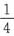xcos2x，y2=sin2x-
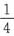xcos2x是某二阶常系数非齐次微分方程的两个解，y3=cos2x是它所对应的齐次方程的一个解，则该微分方程是______．
答案
参考答案：y"+4y=sin2x
解析： 由二阶线性微分方程解的叠加原理可知，y1-y2=cos2x-sin2x是该方程对应的齐次方程(记为(*))的一个解，于是cos2x-(cos2x-sin2x)=sin2x也是方程(*)的解，即(*)有两个线性无关的解cos2x和sin2x，由此可见方程的特征根为±2i，特征方程为r2+4=0，从而知原方程为y"+4y=f(x)．
注意到
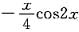是这个方程的一个解，从而f(x)=(
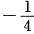xcos2x)"+4(
xcos2x)=sin2x因此，该方程为y"+4y=sin2x．
