参考答案：(x²+6)e^x-3e^2x

解析： 题设二阶常系数线性微分方程的特征方程是λ²+λ-2=0，特征根是λ₁=1与λ₂=-2．从而对应的齐次线性微分方程有线性无关的两个特解e^x与e^-2x，且对应于方程非齐次项f(x)=(6x+2)e^x，可考虑非齐次微分方程具有形状为y^*=x(Ax+B)e^x=(Ax²+Bx)e^x的特解．
把y^*=(Ax²+Bx)e^x，(y^*)’=(Ax²+Bx+2Ax+B)e^x与(y^*)"=(Ax²+bx+4Ax+2B+2A)e^x代入方程可得
(y^*)"+(y^*)’-2y^*=[3(2Ax+B)+2A]e^x

(6x+2)e^x
可确定常数A=1，B=0，故非齐次方程具有特解y^*=x²e^x．
按通解结构定理，应设通解为y=C₁e^x+C₂e^2x+x²e^x，其中C₁与C₂是两个任意常数．利用初值y(0)=3和y’(0)=0可得

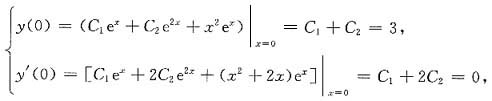
解之即得C₁=6，C₂=-3．故所求特解y^*=(x²+6)e^x-3e^2x．