问题
填空题
设f(x，y)连续，且f(0，0)≠0，又I(R)=
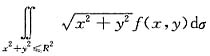当R→0时是关于R的n阶无穷小，则n=______．
答案
参考答案：C
解析： 因f(x，y)连续，积分区域DR={(x，y)|x2+y2≤R2}是闭区域，从而存在f(x，y)在DR上的最小值m(R)与最大值M(R)使得
m(R)≤f(x，y)≤M(R)，(x，y)∈DR，
于是令
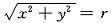，则有
rm(R)≤
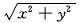f(x，y)≤rM(R)，(x，y)∈DR．
按二重积分的性质即得
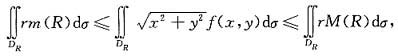
注意
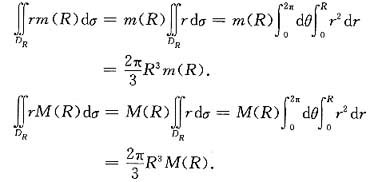
从而
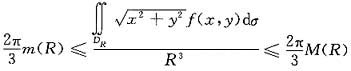
令R→0可得
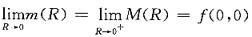，按夹逼定理就有
这表明当R→0时，I(R)关于R是3阶无穷小，即n=3．