问题
填空题
设f(x)=xarctanx-
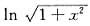 ,则f(x)的幂级数展开式是______.
,则f(x)的幂级数展开式是______.
答案
参考答案:
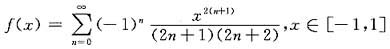
解析: 设g(x)=arctanx则g’(x)=
 (-1)nx2n,x∈(-1,1).
(-1)nx2n,x∈(-1,1).
于是arctanx=g(x)-g(0)=
 g’(t)dt.
g’(t)dt.
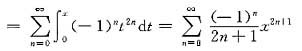
在x=±1处级数
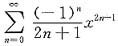 收敛,又函数arctanx在x=±1处连续,所以
收敛,又函数arctanx在x=±1处连续,所以
arctanx=x-
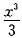 +…+(-1)n
+…+(-1)n
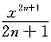 +……,(-1≤x≤1)
+……,(-1≤x≤1)
由ln(1+x)=
 ,(-1<x≤1)得ln(1+x2)=
,(-1<x≤1)得ln(1+x2)=
 ,(-1<x2≤1,即-1≤x≤1)故
,(-1<x2≤1,即-1≤x≤1)故
f(x)=xarctanx-
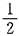 ln(1+x2)
ln(1+x2)
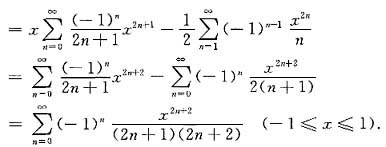
为了求反三角函数或对数函数的幂级数展开式,一般先求它们的导函数的展开式,然后再进行逐项积分;逐项积分时要注意不能忘记积分常数.
