问题
填空题
设y=y(x)是微分方程
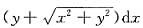=xdy满足初值y(1)=0的特解，则
y(x)dx=______．
答案
参考答案：
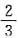
解析： 本题中的方程是齐次微分方程，由初值y(1)=0知应在x＞0处求解．令y=xu可得dy=xdu+udx，代入原方程并化简即得
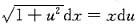，分离变量即得
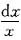．积分知方程的通解为
，从而原方程的通解为
．
由初值y(1)=0可确定常数C=1，从而所求初值问题的特解满足
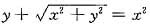．当x＞0时有
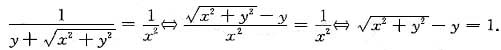
由此可解出满足y(1)=0的特解为y=
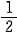(x2-1)．求积分即得
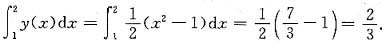
故应填
．
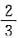