问题
填空题
f(x，y)为连续函数，且f(x，y)=|xy|-
，其中积分区域为D=(x，y)|x2+y2≤1，则f(x，y)的函数表达式为______．
答案
参考答案：
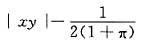
解析： 令A=
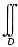f(x，y)dσ，从而f(x，y)=|xy|-A代入即得
A=
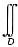f(x，y)dσ=
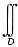(|xy|-A)dσ=
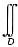|xy|dσ-A
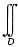dσ．
其中
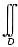dσ=D的面积=π．设D1是D在第一象限的部分区域，即D1={(x，y)|x≥0，y≥0，x2+y2≤1}，利用|xy|分别关于x，关于y是偶函数，故
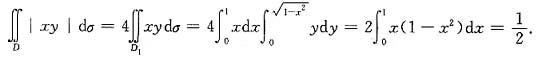
从而A=
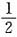-Aπ，即A=
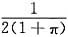．故f(x，y)=|xy|-
．
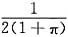