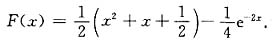问题
填空题
设F(x)=f(x)g(x),其中函数f(x),g(x)在(-∞,+∞)内满足以下条件:f’(x)=g(x),g’(x)=f(x)且f(0)=0,f(x)+g(x)=x+1,则F(x)的表达式是______.
答案
参考答案:
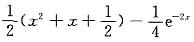
解析: 由于F’(x)=f’(x)g(x)+f(x)g’(x)
=g2(x)+f2(x)
=[f(x)+g(x)]2-2f(x)g(x)
=(x+1)2-2F(x),
故函数F(x)满足一阶线性微分方程F’(x)+2F(x)=(x+1)2.
解该微分方程得
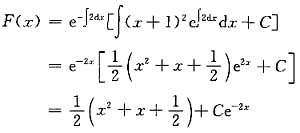
将F(0)=f(0)g(0)=0代入上式得C=
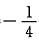
于是