问题
填空题
设幂级数
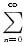anxn的收敛半径为3，则幂级数
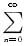nan(x-1)n+1州的收敛区间为______．
答案
参考答案：(-2，4)
解析： 考察两幂级数的关系．令t=x-1，则
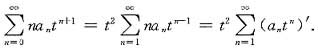
由于逐项求导后的幂级数与原级数有相同的收敛半径，且
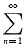anxn的收敛半径为3，所以
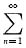(antn)’的收敛半径为3，从而t2
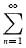(antn)’=
antn+1的收敛半径为3．收敛区间为(-3，3)．回到原级数
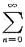nan(x-1)n+1，它的收敛区间为-3＜x-1＜3，即(-2，4)．
请看下面的解法：
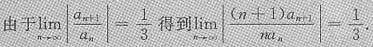
所以
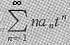的收敛半径为3，从而
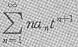的收敛半径R=3，得到了同样的结果．
若作为论证题，上面的证明是错误的，我们知道，对于
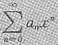，若
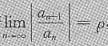，则它的收敛半径是
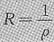．但是若只知它的收敛半径为
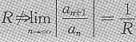．因为
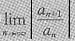可以不存在(对于缺项幂级数就是这种情形)．
但是，上面的讨论对于选择题成填空题也有可取之处，它是在加强了条件(设
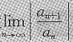存在，原题无此假设)的情形下得出了正确的结果，因而可以选上或填上正确答案．