问题
填空题
设函数f(x)在区间[0，1]上连续，且
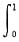f(x)dx=A，则二重积分
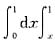f(x)f(y)dy=______．
答案
参考答案：
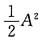
解析： 记
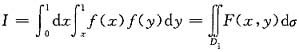，则积分区域D1={(x，y)|0≤x≤1，x≤y≤1}，F(x，y)=f(x)f(y)．将I中的x与y对换即得
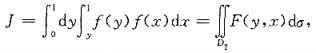
其中积分区域D2={(x，y)|0≤y≤1，y≤x≤1}．不难发现积分区域D1与D2关于直线y=x对称，如图．
由于积分区域D1与D1关于直线y=x对称，被积函数F(x，y)=f(x)f(y)关于自变量x与y对称，即F(x，y)=F(y，x)，从而
