问题
填空题
函数f(x)=ln(3-2x-x2)的麦克劳林展开式为______．
答案
参考答案：
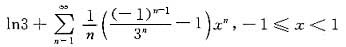
解析： 由3-2x-x2=(3+x)(1-x)知
ln(3-2x-x2)=1n(3+x)+ln(1-x)
展开式的成立范围是-1＜
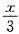≤1与-1≤x＜1的公共部分，即-1≤x＜1．
必须记住五个基本初等函数的麦克劳林展开式：
搜题请搜索小程序“爱下问搜题”
函数f(x)=ln(3-2x-x2)的麦克劳林展开式为______．
参考答案：
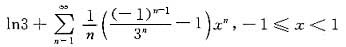
解析： 由3-2x-x2=(3+x)(1-x)知
ln(3-2x-x2)=1n(3+x)+ln(1-x)
展开式的成立范围是-1＜
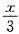≤1与-1≤x＜1的公共部分，即-1≤x＜1．
必须记住五个基本初等函数的麦克劳林展开式：