问题
填空题
交换累次积分的次序可得
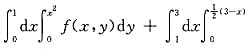f(x，y)dy=______．
答案
参考答案：
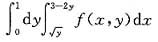
解析： 由题设知对应的二重积分I=
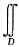f(x，y)dσ的积分区域D=D1+D2，且
D1={(x，y)|0≤x≤1，0≤y≤x2}，
D2={(x，y)|1≤x≤3，0≤y≤
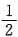(3-x)}，
画出积分区域D如图．由此可见在区域D中最高点的纵坐标为1，最低点的纵坐标为0，左边界的方程是
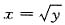，右边界的方程是x=3-2y．从而积分区域D又可表成
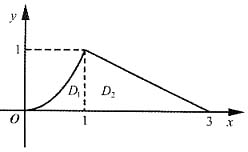
D={(x，y)|0≤y≤1，
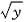≤x≤3-2y}．
故交换积分与次序得
