问题
填空题
把直线y=-x+3向上平移m个单位后,与直线y=2x+4的交点在第一象限,则m的取值范围是______.
答案
方法一:
直线y=-x+3向上平移m个单位后可得:y=-x+3+m,
联立两直线解析式得:
,y=-x+3+m y=2x+4
解得:
,x= m-1 3 y= 2m+10 3
即交点坐标为(
,m-1 3
),2m+10 3
∵交点在第一象限,
∴
,
>0m-1 3
>02m+10 3
解得:m>1.
故答案为:m>1.
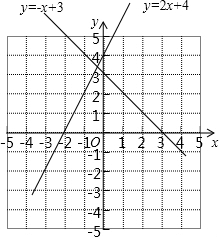
方法二:如图所示:
把直线y=-x+3向上平移m个单位后,与直线y=2x+4的交点在第一象限,
则m的取值范围是m>1.
故答案为:m>1.