问题
解答题
(1)已知f(x)=
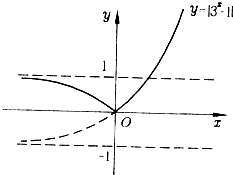
(2)画出函数y=|3x-1|的图象,并利用图象回答:k为何值时,方程|3X-1|=k无解?有一解?有两解? |
答案
(1)因为3x-1≠0⇒x≠0.故函数定义域为{x|x≠0}.
因为函数为奇函数,故有f(-1)=-f(1)⇒
+m=-(2 3-1-1
+m)⇒m=1.2 31-1
所以所求常数m的值为1;
(2)因为函数的零点即为对应两个函数图象的交点.所以把研究零点个数问题转化为研究图象交点个数.
当k<0时,直线y=k与函数y=|3x-1|的图象无交点,即方程无解;
当k=0或k≥1时,直线y=k与函数y=|3x-1|的图象有唯一的交点,所以方程有一解;
当0<k<1时,直线y=k与函数y=|3x-1|的图象有两个不同交点,所以方程有两解.
