（1）对任意实数x，满足f（x）=1-f（x+1）=1-[1-f（x+2）]=f（x+2）=1-f（x+3）=1-[1-f（x+4）]=f（x+4）=…，

也就是有f（x）=f（x+2T），其中T属于z．即f（x）是一个周期为2的周期函数．

对于任意x属于[2k，2k+2]，有x-2k属于[0，2]，则

f（x）=f（x-2k）=|（x-2k）-1|=|x-2k-1|

所以，x∈[2k，2k+2]（k∈Z）时，f（x）=|x-2k-1|

f（x）=|x-2k-1|（2k≤x≤2k+2，k∈Z） 

（2）由（1）可知函数是个周期为2的周期函数，

可将f（x）通式写为f（x）=|x-2k-1|，x∈[2k，2k+2]

取x∈[2k，2k+2]则-x∈[-2k-2，-2k]

那么：f（-x）=|-x-（-2k-1）|=|-x+2k+1|

=|x-2k-1|=f（x） 所以是偶函数．

（3）方程f(x)+log4

log₄ x=|x-2k-1|，x∈[2k，2k+2]，如图

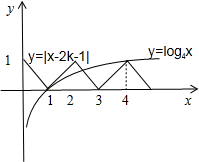
x=4时方程有一个根，x＞4时，方程无根，

方程在[1，4]上有3个实根．