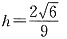问题
问答题
如图所示，存棱长为2的正方体OABC—O1A1B1C1中，E、F分别为棱AB和BC上的动点，且AE=BF.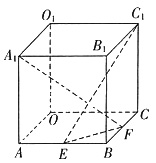
（1）求证：A1F⊥C1E；
（2）当O1B⊥EF时，求点B到平面B1EF的距离.
答案
参考答案：
解：(1)建立如图所示的空间直角生标系O—xyz，设AE=t，则CF=2-t，
∴E点为(2，t，0)，F(2-t，2，0)．
又A1(2，0，2)，C1(0，2，2)，
∴
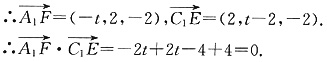
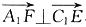，即A1F⊥C1E．
(2)由(1)得O1B=(2，2，-2)，
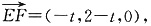
又
，∴-2t+4-2t=0，得t=1.
∴E、F分别为AB、BC的中点．
设点B到平面B1EF的距离为h，由VB-B1EF=VB1-BEF得，