已知函数f(x)是定义域为R的奇函数,且它的图象关于直线x=1对称.
(Ⅰ)求f(0)的值;
(Ⅱ)证明函数f(x)是以4为周期的周期函数;
(Ⅲ)若f(X)=x(0<x≤1),求x∈[-1,3]时,函数f(x)的解析式,求x∈R时,函数f(x)的解析式,并画出满足条件的函数f(x)至少一个周期的图象.
(Ⅰ)∵函数f(x)是奇函数,
∴f(-x)=-f(x).
令x=0,f(0)=-f(0),2f(0)=0,
∴f(0)=0.…(3分)
(Ⅱ)证:∵函数f(x)是奇函数,
∴f(x)=-f(-x)…(1)
又f(x)关于直线x=1对称,
∴f(1+x)=f(1-x).
在(1)中的x换成x+1,即f(1+x)=-f(-1-x),
即f(1-x)=-f(-1-x)…(2)
在(2)中,将1-x换成x,即f(x)=-f(-2+x)…(3)
在(3)中,将x换成2+x,即f(2+x)=-f(x)…(4)
由(3)、(4)得:f(-2+x)=f(2+x).
再将x-2换成x,得:f(x)=f(x+4).
∴f(x)是以4为周期的周期函数.…(8分)
(Ⅲ)设-1≤x<0时,则0<-x≤1,所以f(-x)=-x.
又f(-x)=-f(x),所以f(x)=x,又f(0)=0,
所以,当-1≤x≤1时,f(x)=x.
当1<x<3时,-3<-x<-1,则-1<2-x<1.
所以f(2-x)=2-x,而函数f(x)的图象关于直线x=1对称,
所以f(2-x)=f(x),即f(x)=2-x.
所以x∈[-1,3]时,函数f(x)的解析式为:f(x)=x,-1≤x≤1 -x+2,1<x≤3
再由f(x)是以4为一个周期的周期函数,
从而有x∈R时,函数f(x)的解析式为:f(x)=
(k∈Z),x-4k,4k-1≤x≤4k+1 -x+2+4k,4k+1<x<4k+3
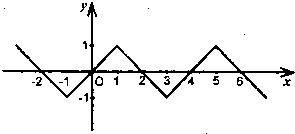
函数f(x)一个周期的图象如图所示.…(13分)

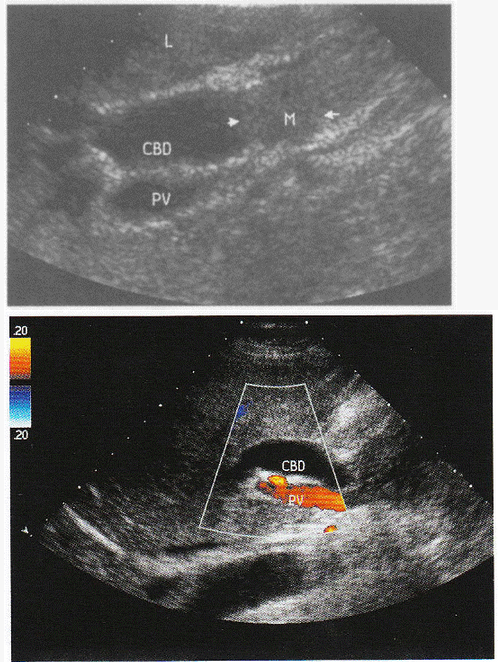 超声提示()
超声提示()