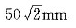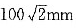问题
解答题
| 设y=f(x)是定义在区间[-1,1]上的函数,且满足条件,①f(-1)=f(1)=0,②对任意的u、v∈[-1,1],都有|f(u)-f(v)|≤|u-v| (Ⅰ)证明:对任意x∈[-1,1],都有x-1≤f(x)≤1-x (Ⅱ)证明:对任意的u,v∈[-1,1]都有|f(u)-f(v)|≤1 (Ⅲ)在区间[-1,1]上是否存在满足题设条件的奇函数y=f(x)且使得
|
答案
(Ⅰ)证明:由题设条件可知,
当x∈[-1,1]时,有|f(x)|=|f(x)-f(1)|≤|x-1|=1-x,即x-1≤f(x)≤1-x.
(Ⅱ)证明:对任意的u,v∈[-1,1],
当|u-v|≤1时,有|f(u)-f(v)|≤|u-v|≤1
当|u-v|≤1时,u•v<0,不妨设u∈[-1,0),v∈(0,1],则v-u>1
从而有|f(u)-f(v)|≤|f(u)-f(-1)|+|f(v)-f(1)|≤|u+1|+|v-1|=2-(v-u)<1
综上可知,对任意的u,v∈[-1,1],都有|f(u)-f(v)|≤1
(Ⅲ)这样满足所述条件的函数不存在.理由如下:
假设存在函数f(x)满足条件,则由|f(u)-f(v)|=|u-v|.
u,v∈[
,1]得|f(1 2
)-f(1)|=|1 2
-1|=1 2 1 2
又f(1)=0,所以|f(
)|=1 2
①1 2
又因为f(x)为奇函数,所以f(0)=0,
由条件|f(u)-f(v)|<|u-v|.
u,v∈[0,
]得|f(1 2
)|=|f(1 2
)-f(0)|<|1 2
-0|=1 2 1 2
所以|f(
)|<1 2
②1 2
①与②矛盾,因此假设不成立,即这样的函数不存在.

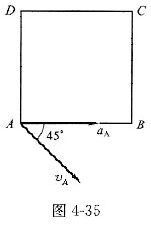
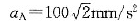 ,方向如图4-35所示,则该板转动轴到A点的距离OA为()。
,方向如图4-35所示,则该板转动轴到A点的距离OA为()。