（Ⅰ）由题设，g（x）=x²-alnx，

则g′(x)=2x-

a

x

．（1分）

由已知，g'（1）=0，

即2-a=0⇒a=2．（2分）

于是h(x)=x-2

x

，

则h′(x)=1-

1

x

．（3分）

由h′(x)=1-

1

x

＞0⇒x＞1，

所以h（x）在（1，+∞）上是增函数，在（0，1）上是减函数．（4分）

证明：（Ⅱ）当1＜x＜e²时，0＜lnx＜2，

即0＜f（x）＜2．（5分）

欲证x＜

2+f(x)

2-f(x)

，

只需证x[2-f（x）]＜2+f（x），

即证f(x)＞

2(x-1)

x+1

．（6分）

设φ(x)=f(x)-

2(x-1)

x+1

=lnx-

2(x-1)

x+1

，

则φ′(x)=

1

x

-

2(x+1)-2(x-1)

(x+1)2

=

(x-1)2

x(x+1)2

．

当1＜x＜e²时，φ'（x）＞0，

所以φ（x）在区间（1，e²）上为增函数．（7分）

从而当1＜x＜e²时，φ（x）＞φ（1）=0，

即lnx＞

2(x-1)

x+1

，

故x＜

2+f(x)

2-f(x)

．（8分）

（Ⅲ）由题设，h1(x)=x-2

x

+6．

令g（x）-h₁（x）=0，

则x2-2lnx-(x-2

x

+6)=0，

即2

x

-2lnx=-x2+x+6．（9分）

设h2(x)=2

x

-2lnx，

h₃（x）=-x²+x+6（x＞0），

则h2′(x)=

1

x

-

2

x

=

x -2

x

，

由

x

-2＞0，得x＞4．

所以h₂（x）在（4，+∞）上是增函数，

在（0，4）上是减函数．（10分）

又h₃（x）在（0，

1

2

）上是增函数，

在（

1

2

，+∞）上是减函数．

因为当x→0时，h₂（x）→+∞，h₃（x）→6．

又h₂（1）=2，h₃（1）=6，h₂（4）=4-2ln4＞0，h₃（4）=-6，

则函数h₂（x）与h₃（x）的大致图象如下：（12分）

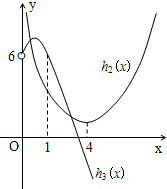
由图可知，当x＞0时，两个函数图象有2个交点，

故函数y=g（x）-h₁（x）有2个零点．（13分）