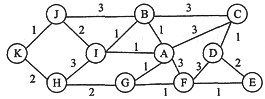
一个网络的拓扑结构如下图所示。链路旁边注明的数字代表链路的长度(假想单位)。试利用链路状态路由算法求出从结点A到所有其他结点的最短路由,给出计算过程,最短路径图以及下一跳路由。
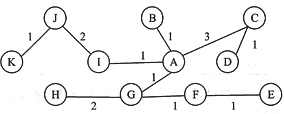
参考答案:本题利用Dijkstra算法求出最短路径树(下图),从而得到结点A路由表(表2)。计算过程如表1所列。
| 表1 | |||||||||||
| 步骤 | N | S(B) | S(C) | S(D) | S(E) | S(F) | S(G) | S(H) | S(I) | S(G) | S(K) |
| 初始化 | {A} | 1 | 3 | ∞ | ∞ | 3 | 1 | ∞ | 1 | ∞ | ∞ |
| 1 | {A,B} | 1 | 3 | ∞ | ∞ | 3 | 1 | ∞ | 1 | 4 | ∞ |
| 2 | {A,B,G} | 1 | 3 | ∞ | ∞ | 2 | 1 | 3 | 1 | 4 | ∞ |
| 3 | {A,B,G,I} | 1 | 3 | ∞ | ∞ | 2 | 1 | 3 | 1 | 3 | ∞ |
| 4 | {A,B,G,I,F} | 1 | 3 | 5 | 3 | 2 | 1 | 3 | 1 | 3 | ∞ |
| 5 | {A,B,G,I,F,C} | 1 | 3 | 4 | 3 | 2 | 1 | 3 | 1 | 3 | ∞ |
| 6 | {A,B,G,I,F,C,E} | 1 | 3 | 4 | 3 | 2 | 1 | 3 | 1 | 3 | ∞ |
| 7 | {A,B,G,1,F,C,E,H} | 1 | 3 | 4 | 3 | 2 | 1 | 3 | 1 | 3 | 5 |
| 8 | {A,B,G,I,F,C,E,H,J} | 1 | 3 | 4 | 3 | 2 | 1 | 3 | 1 | 3 | 4 |
| 9 | {A,B,G,I,F,C,E,H,J,D} | 1 | 3 | 4 | 3 | 2 | 1 | 3 | 1 | 3 | 4 |
| 10 | {A,B,G,I,F,C,E,H,J,D,K} | 1 | 3 | 4 | 3 | 2 | 1 | 3 | 1 | 3 | 4 |
| 表2 结点A的路由表 | ||||||||||
| 目标结点 | B | C | D | E | F | G | H | I | J | K |
| 后继结点 | B | C | C | G | G | G | G | I | I | I |
解析: 本题考查链路状态路由算法的基本原理,每个结点利用可靠的方法获知其邻居节点以及到各邻居结点的链路的代价,通过与网络内其他结点交换这些信息来获得关于全网的拓扑信息,即网中所有的节点、链路和链路的代价,将这些拓扑信息抽象成一张带权图,然后用图论的方法计算出到各个目的结点的最短路径。链路状态路由算法包括以下五个部分:发现邻居,获知邻居的网络地址;测量到每个邻居的延时;将以上信息构造成链路状态分组;向所有结点发送链路状态分组;计算到每个节点的最短路径。Dijkstra算法是一种求单源最短路径树的算法,是链路状态路由协议的核心算法,该算法基本原理是:每次新扩展一个距离最短的点,更新与其相邻的点的距离。当所有边权都为正时,由于不会存在一个距离更短的没扩展过的点,所以这个点的距离永远不会再被改变,因而保证了算法的正确性。在以下算法中,s为源,w[u,v]为点u和v之间的边的长度,结果保存在dist[]。
(1)初始化:源的距离dist[s]设为0,其他的点距离设为无穷大,同时把所有的点的状态设为没有扩展过。
(2)循环n-1次:在没有扩展过的点中取一距离最小的点u,并将其状态设为已扩展。
对于每个与u相邻的点v,执行Relax(u,v),也就是说,如果dist[u]+w[u,v]<dist[v],那么把dist[v]更新成更短的距离dist[u]+w[u,v]。此时到点v的最短路径上,前一个结点即为u。
(3)结束。此时对于任意的u,dist[u]就是s到u的距离。
