问题
问答题
设A是n阶正定矩阵，α1，α2，α3是非零的n维列向量，且
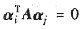(i≠j，i，j=1，2，3)．证明α1，α2，α3线性无关．
答案
参考答案：[证明] 设k1α1+k2α2+k3α3=0，用[*]左乘，得
[*]．
因为 [*]．
由A正定且α1≠0知，[*]，从而k1=0．
同理可证k2=0，k3=0，所以α1，α2，α3线性无关．
搜题请搜索小程序“爱下问搜题”
设A是n阶正定矩阵，α1，α2，α3是非零的n维列向量，且
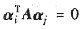(i≠j，i，j=1，2，3)．证明α1，α2，α3线性无关．
参考答案：[证明] 设k1α1+k2α2+k3α3=0，用[*]左乘，得
[*]．
因为 [*]．
由A正定且α1≠0知，[*]，从而k1=0．
同理可证k2=0，k3=0，所以α1，α2，α3线性无关．