问题
解答题
已知数列{an}是首项为1,公比为q(q>0)的等比数列,并且2a1,a3,a2成等差数列。
(1)求q的值;
(2)若数列{bn}满足bn=an+n,求数列{bn}的前n项和Tn。
答案
解:(1)由a3=2a1+a2,得q2=2+q
∴q=2,q=-1(舍去)
∴an=1×2n-1=2n-1。
(2)∵an=2n-1,
∴bn=2n-1+n
∴Tn=(1+2+22+23+…+2n-1)+(1+2+3+…+n)=2n-1+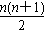 。
。
