已知真空中电量为Q的点电荷电场中,若取无穷远为零电势点,则离电荷距离为r的某点的电势表达式为φ=
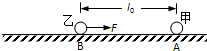
(k为静电力常数).如图所示,带正电的甲球固定在足够大的光滑绝缘水平面上的A点,其带电量为Q;质量为m、带正电的乙球在水平面上的B点由静止释放,其带电量为q;A、B两点间的距离为l0.释放后的乙球除受到甲球的静电力作用外,还受到一个大小为F=kQ r
、方向指向甲球的恒力作用,两球均可视为点电荷.求:kQq 4l02
(1)乙球在释放瞬间的加速度大小;
(2)乙球的速度最大时两个电荷间的距离;
(3)乙球运动的最大速度vm为多少?
(4)乙球运动过程中,离开甲球的最大距离和最小距离是多少?
(1)乙球受到电场力和F的作用,根据牛顿第二定律得
K
=maqQ l 20
解得,a=3kqQ 4m l 20
(2)乙球的合外力先向左,所以乙球向左做加速度减小的加速运动,当合力为零时,速度最大,则有
K
-KqQ r2
=0qQ 4 l 20
解得 r=2l0
(3)乙球的电势能:ε=qϕ=
,电场力做正功,等于电势能的减少:kqQ r
WE=-△ε=-(K
-KqQ 2l0
)=kqQ l 0 qQ 2l0
外力做负功:WF=-K
l0=-KqQ 4 l 20 Qq 4l0
由动能定理:WE+WF=
m1 2
-0V 2m
得:
=V m kqQ 2ml0
(4)乙球达到速度最大后,再向左做加速度增大的减速运动,当速度等于零时,离甲球最远.V=0此时离开甲球距离为rm,然后又向右运动,根据对称性可知,当r=l0时速度又等于零.所以离开A球最近的距离为l0.
根据动能定理得 WE+WF=0
-kqQ rm
=-kKqQ l0
(rm-l0)qQ 4 l 20
解得,rm=4l0
答:
(1)乙球在释放瞬间的加速度大小是
;3kqQ 4m l 20
(2)乙球的速度最大时两个电荷间的距离是2l0;
(3)乙球运动的最大速度vm为
.kqQ 2ml0
(4)乙球运动过程中,离开甲球的最大距离4l0,最小距离是l0.
