问题
解答题
已知函数f(x)是定义在[-e,0)∪(0,e]上的奇函数,当x∈[-e,0)时,f(x)=ax-ln(-x),(a<0,a∈R)
(I)求f(x)的解析式;
(Ⅱ)是否存在实数a,使得当x∈(0,e]时f(x)的最大值是-3,如果存在,求出实数a的值;如果不存在,请说明理由.
答案
(I)设x∈(0,e],则-x∈[-e,0).
而f(x)是奇函数,∴f(x)=-f(-x)=-[a(-x)-lnx]=ax+lnx.
∴f(x)=
.ax-ln(-x),x∈[-e,0) ax+lnx,x∈(0,e]
(II)假设存在实数a,使得当x∈(0,e]时f(x)的最大值是-3.
f′(x)=a+
=1 x
,ax+1 x
(i)当-
≥e时,即-1 a
≤a<0时.f(x)在(0,e]上是增函数,1 e
∴f(x)max=f(e)=ae+1=-3,解得a=
<--4 e
,应舍去.1 e
(ii)当-
<e时,即a<-1 a
时.1 e
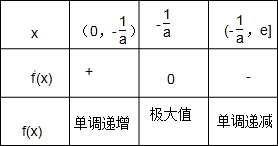
列表
由表格可知:f(-
)=-1+ln(-1 a
)=-3,得a=-e2.1 a
故存在实数a=-e2,使f(x)在(0,e]上取得最大值-3.
