问题
解答题
已知数列{an}和{bn}的通项公式分别为an=3n+6,bn=2n+7(n∈N*),将集合{x|x=an,n∈N*}∪{x|x=bn,n∈N*}中的元素从小到大依次排列,构成数列c1,c2,c3,…cn。
(1)求三个最小的数,使它们既是数列{an}中的项,又是数列{bn}中的项;
(2)c1,c2,c3,…c40中有多少项不是数列{bn}中的项?说明理由;
(3)求数列{cn}的前4n项和S4n(n∈N*)。
答案
解:(1)三项分别为9,15,21;
(2)数列c1,c2,c3,…,c40的项分别为:
9,11,12,13,15,17,18,19,21,23,24,25,27,29,30,31,33,35,36,37,39,41,42,43,45,47,48,49,51,53,54,55,57,59,60,61,63,65,66,67,则不是数列{bn}中的项有12,18,24,30,36,42,48,54,60,66共10项;
(3) ,
,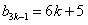 ,
, ,
,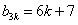
∵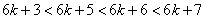
∴ ,
,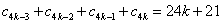
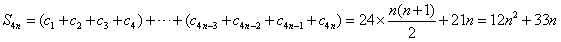 。
。
