证明：(Ⅰ)易知1²，5²，7²成等差数列，则a²，(5a)²，(7a)²也成等差数列，

所以对任一正整数a，都存在正整数b=5a，c=7a(b＜c)，使得a²，b²，c²成等差数列．

(Ⅱ)若a_n²，b_n²，c_n² 成等差数列，则有b_n²-a_n²=c_n²-b_n²，

即(b_n-a_n)(b_n+a_n)=(c_n-b_n)(c_n+b_n)， ①

选取关于n的一个多项式，例如4n(n²-1)，使得它可按两种方式分解因式，

由于4n（n²-1）=(2n-2)(2n²+2n)=(2n+2)(2n²-2n)，

因此令，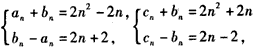

可得，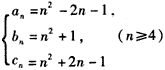

易验证a_n，b_n，c_n满足①，因此a_n²，b_n²，c_n² 成等差数列，

当n≥4时，有a_n＜b_n＜c_n且a_n+b_n-c_n=n²-4n+1＞0，

因此以a_n，b_n，c_n为边长可以构成三角形，将此三角形记为△_n(n≥4)．

其次，任取正整数m，n（m，n≥4，且m≠n），假若三角形△_m与△_n相似，

则有，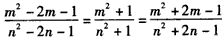

据比例性质有，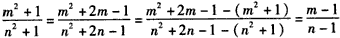

，

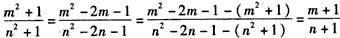所以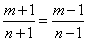，由此可得m=n，与假设m≠n矛盾，

即任两个三角形△_m与△_n(m，n≥4，m≠n)互不相似；

所以存在无穷多个互不相似的三角形△_n，其边长a_n，b_n，c_n为正整数且a_n²，b_n²，c_n² 成等差数列。